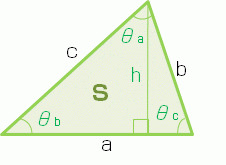
H (高さ)の式がおかしい。 3つともh=2S/aでなければおかしい。 例a=6,b=7,c=10で計算結果がA=3618・・,B=4353・・,C=・・,h=6・・,S=66・・if c>=a,bの場合はh=2S/cになっているが、2*66/10=413・・になってしまう。 keisanより 表記しているhは、それぞれa,b,cを底辺としたときの高さとなります。 a >= b,cの時、aを底辺としたときの高さhb >= c,aの時、bを底辺としたときの高さ不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺aと角C 面積と高さと角C本で持ち運びたいなら ⇒参考書「逆転の高校数学Ⅰ」 http//ur0work/CZOt ・twitter(@yarukisensei) https//twittercom/yarukisensei

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
不等辺三角形 辺の長さ 比
不等辺三角形 辺の長さ 比-互いに合同な直角二等辺三角形を複数配置することで正三角形の作図が可能である。 辺の長さが1,1, の直角二等辺三角形を用いて一辺の長さが2となる正三角形を作図できる。 底辺の長さが で高さが1の直角三角形の斜辺の長さが となることを応用する。不等辺三角形 著者名 著:内田 康夫 発売日 12年04月06日 価格 定価:1,122円(本体1,0円) isbn 9754 判型 新書 ページ数 296ページ シリーズ 講談社ノベルス 初出 10年4月に小社より単行本として刊行されたものを、ノベルス化したもの。




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思いますがすなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc;三角不等式は様々な「長さ」に拡張されています。→いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc
直角三角形の辺の長さを求める問題(三角測量の問題)においては,必要な三角比の値が分かっていなければなりませんが,次の3種類×3の値は問題文に書かれていなくても読者が覚えていなければなりません. これ以外の値,例えば sin 22°などが必要に直角三角形の2 辺の長さがわかれば,残りの辺の長さは,三平方の定理を利用して求めるこ とができる。直角をはさむ2 辺の長さをa,bとし,斜辺の長さをcとすると ・a,bが与えられたとき cab=+22 ・b,cが与えられたとき acb=-22 三平方の定理の逆 三角形の3 辺の長さa,b,cの間に 直角三角形の辺の比の3つのパターン 直角三角形の比は3つ覚えればいい?? こんにちは!ぺーたーだよ。 三平方の定理で覚えておきたいのは、 直角三角形の比 だよ。 これを覚えておけば、 三平方の定理を使わなくて辺の長さを計算できちゃうんだ。
H=S/ (a/2)より、 h=a・sin (θ1)・sin (θ2)/sin (θ1θ2) =a・sin (θ1)・sin (θ2)/ (sin (θ1)・cos (θ2)cos (θ1)・sin (θ2)) =a・tan (θ1)・tan (θ2)/ (tan (θ1)tan (θ2)) となり、hの式は合っていると考えられます。 Lの式については、ご指摘ありがとうございます。 Lだけhを使用しているので、後ほど修正(入力パラメータのa,θ1,θ2のみ使用)いたします。 2 1652 男 / 60歳以上残り2辺の長さを求めることができます。 もちろん \(11\sqrt{2}\)や\(12\sqrt{3}\)という比は覚えておく必要があるからね。 しっかりと覚えておこう! では、特別な直角三角形において 比を使いながら辺の長さを求める練習をしていきましょう。1辺の長さを a 、その両端角の角度を B, C とするとき、面積 S は S = a 2 sin B sin C 2 sin ( B C) {\displaystyle S= {\frac {a^ {2}\sin B\sin C} {2\sin (BC)}}} ・・・⑤ または S = a 2 2 ( cot B cot C) {\displaystyle S= {\frac {a^ {2}} {2 (\cot B\cot C)}}} ・・・⑥ で求められる。



三角比と辺の長さの関係は 1分でわかる求め方 角度と辺の長さの比




底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo
3辺の長さだけがわかっている三角形の面積を求めるには、 (1)一旦、余弦定理で、ある角の cos を求める (2)次に sin 2 θ+cos 2 θ=1 の関係を使って sin を求める (3)2辺とその間の角の sin が判明したので、これを公式に当てはめる アプリもご利用三角形を成り立たせる3辺 (三角形の成立条件) 三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc;三角比のセンター試験問題 → 携帯版は別頁 三角形を解くとは 三角形には3つの角と3つの辺があります.これらの内の幾つかの要素が与えられたとき,残りの要素を求めることを「 三角形を解く 」といいます. 相似図形の性質を考えると分かるように



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




2が無理数であることの図形的な証明 理系のための備忘録
三角形の2辺の和と差 物理学のフィロ 直角三角形の高さは?1分でわかる計算、求め方、公式、直角二等辺三角形の辺の長さ 直角三角形の辺の比の関係 理数系無料オンライン学習 kori 三角形 三角形の概要 ナビゲーションに移動検索に移動この項目では、図形について説明しています。記号文字については「三角 (記号)」をご覧ください。 三角形目次1 記法・定義11 三角形を成り立たせる3辺 (三角形の成立条計算すると、 4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 (二乗して 13 になる正の数)となります。 では、 13 はどれくらいの長さでしょうか? 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
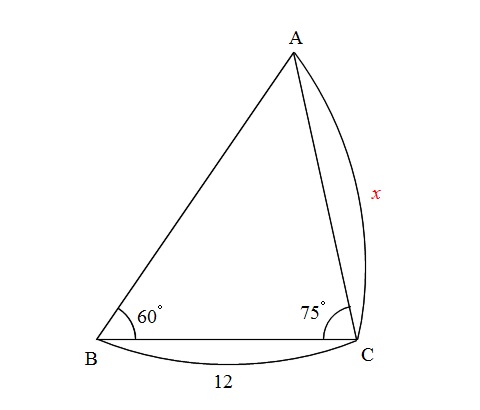



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
不等辺三角形の面積を計算する方法 その他のセクション 辺と角度が等しくない三角形は、不等辺三角形と呼ばれます。 この種の三角形の領域を把握する方法は3つありますが、使用する方法は、解決しようとしている問題で指定されている値によって2 高さ (h) =SQRT (3)/2*B1 3 3辺の長さ (L) =3*B1 4 面積 (S) =SQRT (3)/4*B1^2三角形の3辺が与えられたときの面積の求め方 「3辺の長さが,5,4,7の三角形の面積を求めよ。」という問題がわかりません。面積を求めるときは,公式 S=1/2bc sinA に当てはめればいいことは



三角形の計算 Google Play のアプリ




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
直角三角形の辺の長さの比で、√3や√2がどこから出てきているのかわかりません。 三辺の長さがわかっている三角形の面積の出し方。 三平方の定理を利用して 方程式 をつくり、高さを求める。 abcの二等辺三角形 (にとうへんさんかくけい、 英 isosceles triangle )は、 三角形 の一種で、3 本の 辺 のうち(少なくとも)2 本の辺の長さが等しい 図形 である。 長さの等しい 2 辺を 等辺 といい、残りの 1 辺を 底辺 とよぶ。 2 本の等辺が共有する頂点をとくに二等辺三角形の 頂点 という。 頂点における内角を、二等辺三角形の 頂角 といい、残りの 2 つの 三辺の長さが等比数列となる三角形の存在条件 数学 本記事では、三辺の長さがそれぞれx,x 2 ,x 3 (初項x、公比xの 等比数列 でx>0)である三角形の存在条件について考えます。 少しネタバレすると、有名な「美しい比率」が登場します。




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




14 号 図形板セット Astamuse
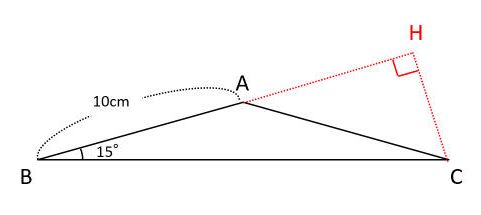
このように,相似な三角形は対応する辺の比が等しいので,辺の比さえ分かってしまえば, どのように大きな三角形の辺の長さも,すぐに求めることができる。 直角三角形の場合,直角以外の1 つの角が決まると相似となるので,正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりまBH=xとおいて (このときCH=6xとなります) AHの長さ (の2乗)を2とおりの方法で表わせば解けます。 (√13) 2 x 2 = AH 2 = 5 2 (6x) 2 (√13)2x2 = 52 (6x)2 13x 2 =25 (3612xx 2 ) 24=12x x=2 (√13) 2 2 2 =AH 2 AH=3




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
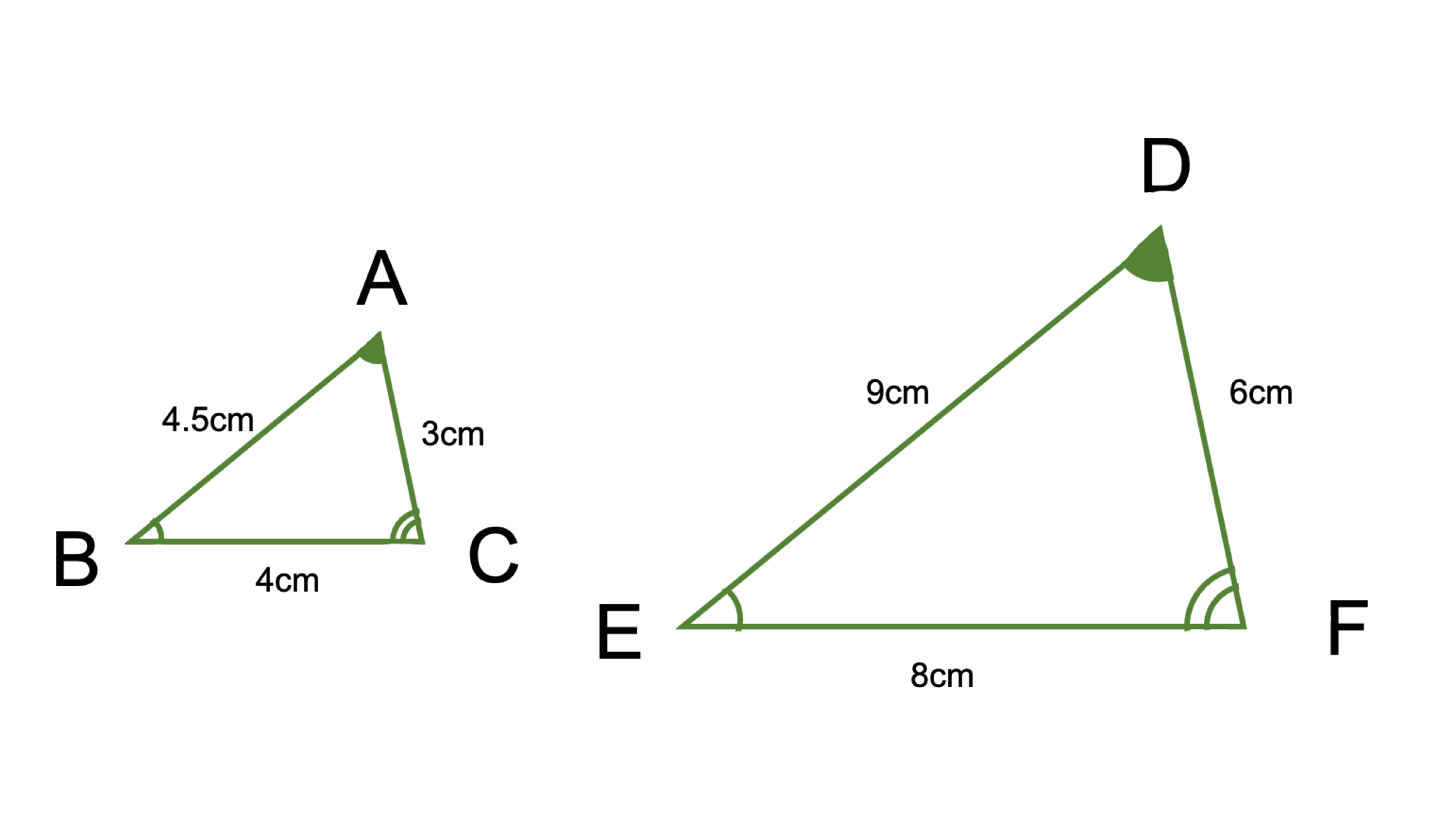



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
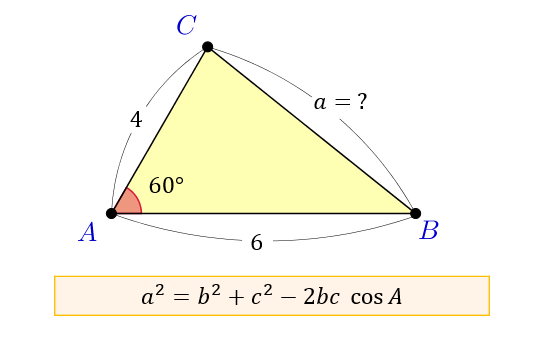
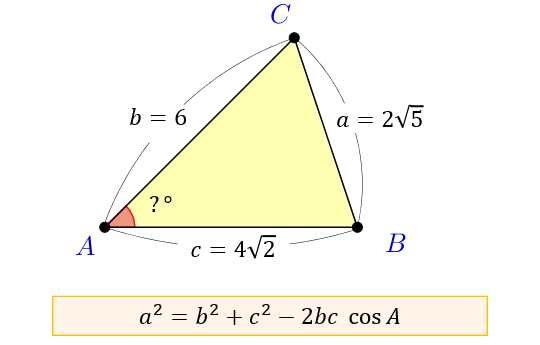
余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますが三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角形 辺 の 長 さ 比率 238n424 Proxydns Com




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




辺の長さが全て整数で 周の長さと面積が等しくなる直角三角形と二等辺三角形は一組しか無い あみこども未来ラボ




直角二等辺三角形 Wikipedia




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
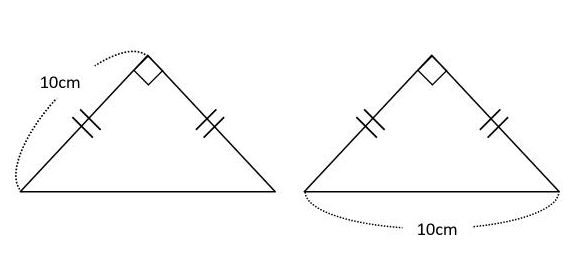



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
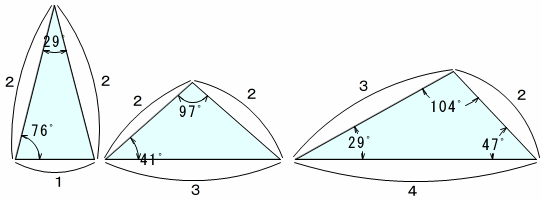



3 4 5の三角形で 本当に直角ができる Note Board
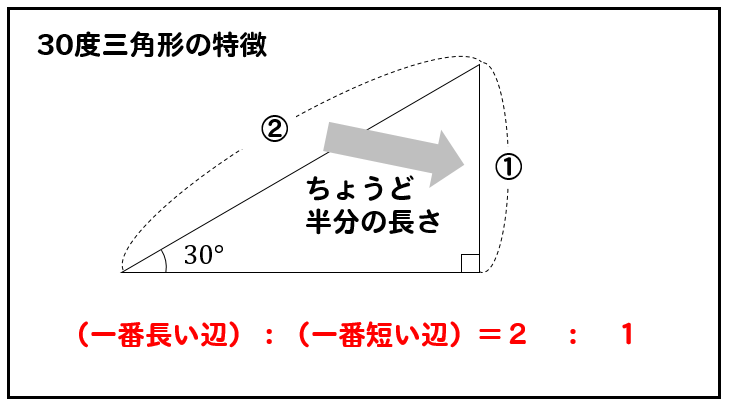



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
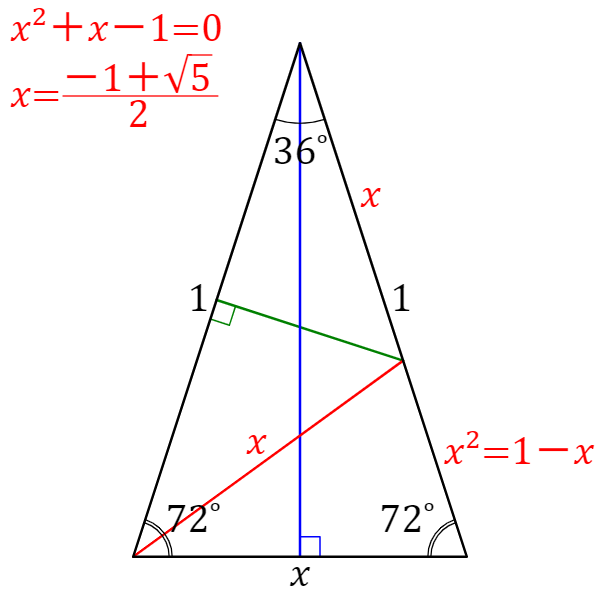



Sin18 Cos72 Cos36 Sin54 を簡単に求める方法 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




直角三角形 Wikipedia
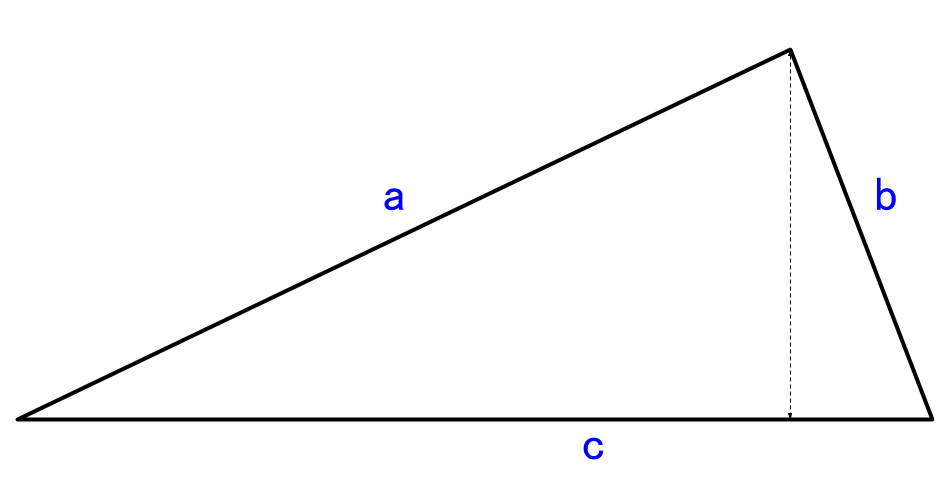



ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学



三角形の公式 Wakatta



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
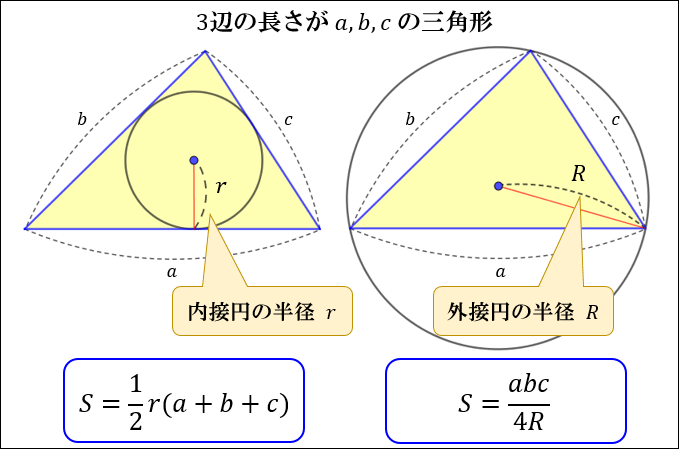



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三角比を考え方から理解する 有名角の三角比も説明



ゆっるゆる アクアリウムと日本の庭園にみる伝統石組みレイアウト Mobi Aqua
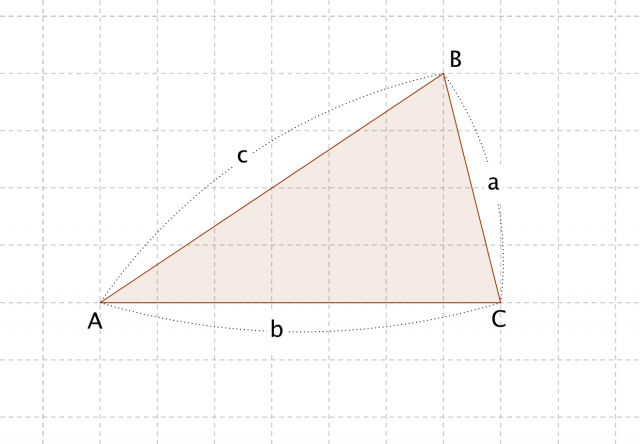



C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
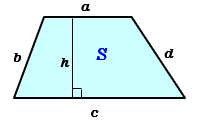



計算
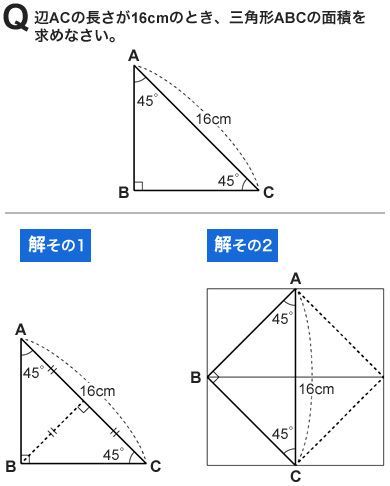



ベストコレクション 不等辺三角形 高さ 求め方 不等辺三角形 高さ 求め方 小学生




数学 中3 61 三平方の定理 基本編 Youtube




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
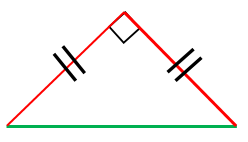



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
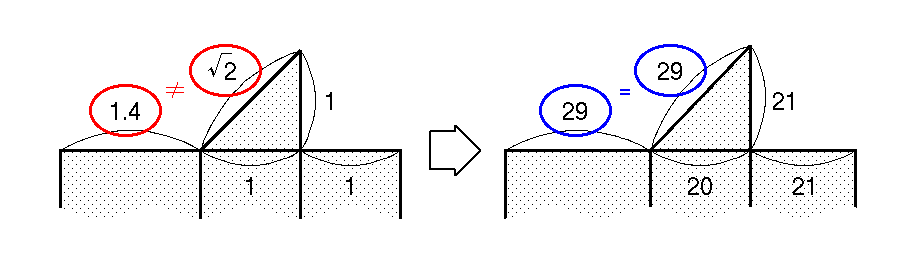



ピタゴラスの三角形




ベストコレクション 不等辺三角形 高さ 求め方 不等辺三角形 高さ 求め方 小学生



不等辺三角形角度について教えて下さい 辺aが1367辺bが473 Yahoo 知恵袋



3



直角 三角形 の 重心
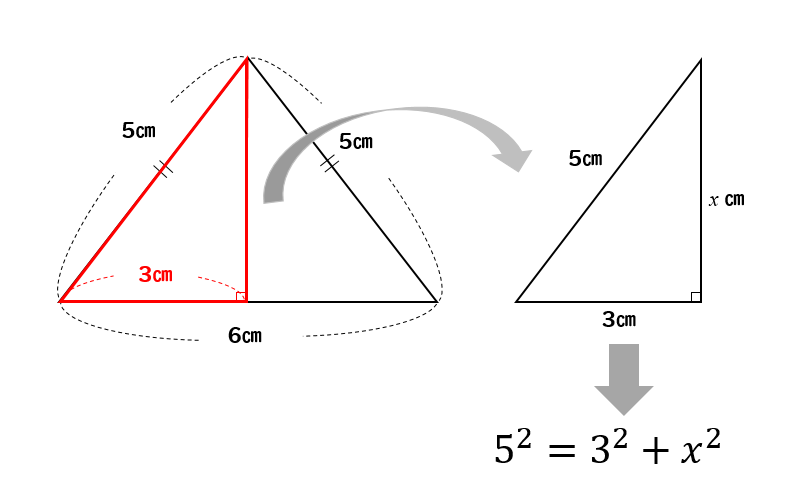



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
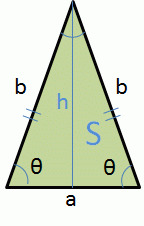



三角形の公式 Wakatta




任意の三角形は二等辺三角形である Fukusukeの数学めも




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
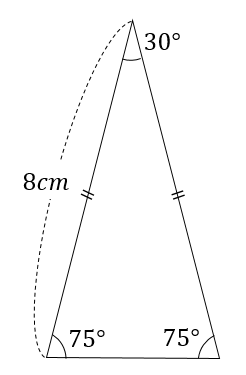



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




三平方の定理の応用



1



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




直角三角形 Wikiwand




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
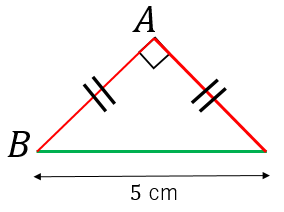



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
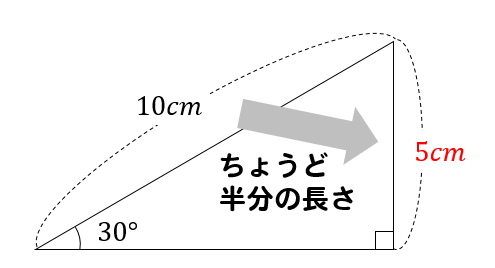



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ



Www Kyoiku Shuppan Co Jp Tsushin Files 17st 04sugaku Pdf
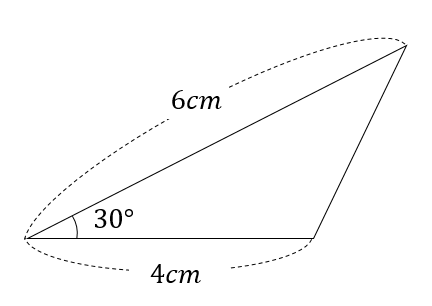



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ



直角二等辺三角形の長さが等しい2辺と斜辺にはどのような関係がありますか Quora



直角 三角形 の 重心
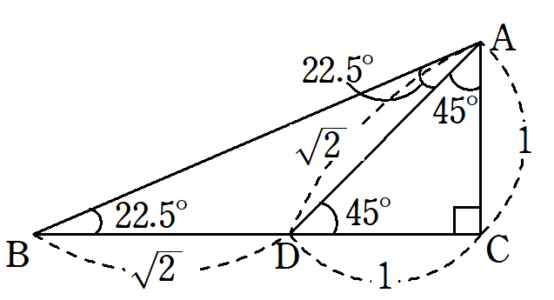



22 5 の三角比 Fukusukeの数学めも




三角比 30 45 60 もう一度やり直しの算数 数学
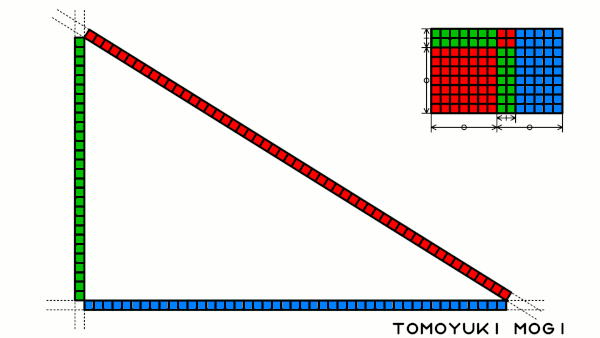



直角三角形 Wikiwand



覚えて損はない 直角三角形の辺の比の3つのパターン Qikeru 学びを楽しくわかりやすく




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




黄金三角形による18 シリーズの三角比 おいしい数学




画像の比の直角三角形は 直角三角形で 1つの辺の長さ 比 が 又は であ Clear




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




ベストコレクション 不等辺三角形 高さ 求め方 不等辺三角形 高さ 求め方 小学生




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
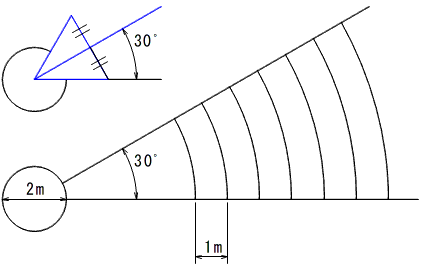



3 4 5の三角形で 本当に直角ができる Note Board




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



三角形の辺の比
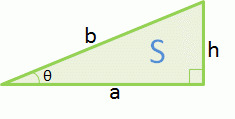



三角形の公式 Wakatta




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



不等辺三角形角度について教えて下さい 辺aが1367辺bが473 Yahoo 知恵袋




1 の問題で 自分の証明でも合ってますか 字が汚くてすいません Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



正三角形 二等辺三角形 直角三角形の書き方 作図 まとめ 受験辞典




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




直角三角形の辺を求める Youtube




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




直角二等辺三角形 Wikiwand




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
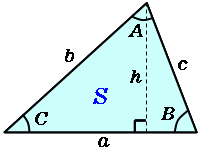



不等辺三角形 高精度計算サイト




黄金三角形による18 シリーズの三角比 おいしい数学
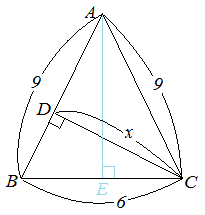



三平方の定理の応用



黄金三角形 Wikipedia
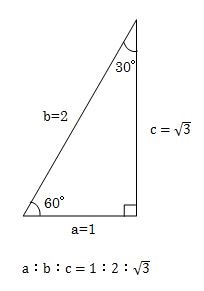



三角比 30 45 60 もう一度やり直しの算数 数学



3
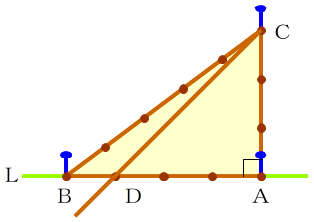



3 4 5の三角形で 本当に直角ができる Note Board
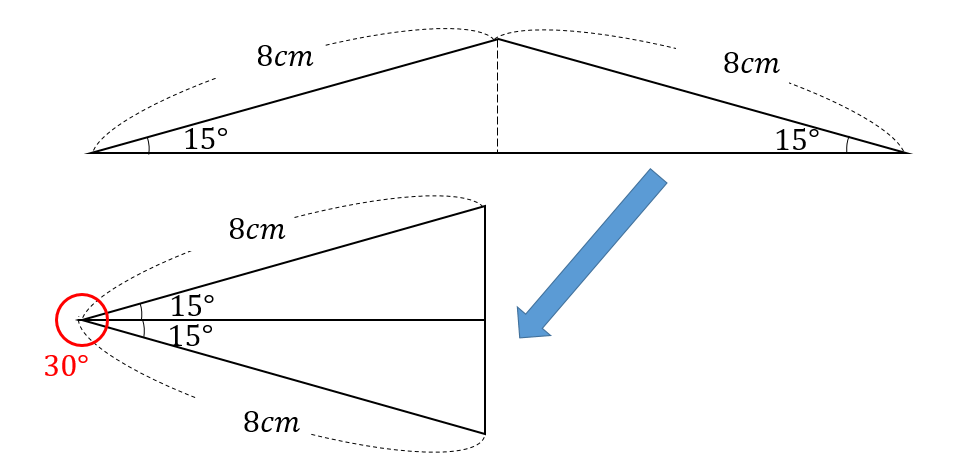



小学算数 15度 75度の三角形ってどうやって面積求める 数スタ




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



Q Tbn And9gcryolrm Dxfwat4p1nhc1gjbk0qzj6wrbkjapaspbruhs7arqz3 Usqp Cau




直角三角形 Wikiwand
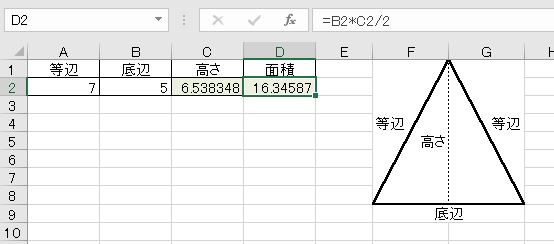



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




黄金三角形による18 シリーズの三角比 おいしい数学
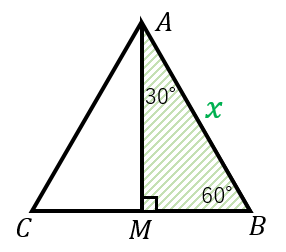



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



0 件のコメント:
コメントを投稿